▶ 영재교육 (45)21세기 우리아이들...어떻게 기를까
▶ 전정재 박사
"우리아이는 학교에서 따로 수학 공부를 시킬 정도로 수학을 아주 잘 합니다. 계산만이 아니고 응용문제도 정말 잘하고 또 자기도 수학을 무척 좋아합니다. 그런데 이상하게도 저학년 때부터 완전히 100점을 맞아오지는 못합니다. 성격이 그리 덤벙거리지도 않거든요. 그것보다도 걱정이 되는 것은 요즘 수학을 많이 틀려오는 것을 보면 몰라서나 응용문제를 파악하지 못하는 것도 아닌데 더하기(+) 할 때를 빼기(-)를 한다든지… 자기 말로도 ‘바보 같은 행동’(stupid mistakes)이라고 인정을 하기는 합니다. 어려운 것은 오히려 다 맞아옵니다. 고학년으로 올라갈수록 이런 것이 더 심해져 가는데, 어떻게 도와 줄 길이 없을까요?"
-7학년 영진이 어머니
■해결책: 위의 예는 고학년이 되면서 수학 문제를 잘 이해하지 못하는 데서 오는 현상이다. 이런 문제를 해결할 수 있는 학습법을 소개하려고 한다, 즉 SQRQCQ 방법이다. 이 방법은 계산 능력과 관련된 것은 제외하고, 응용문제에만 적용된다. 이 방법을 이용하려면 두 가지 준비과정이 있다.
I. 준비과정
A. 클로즈 리딩(close reading)
B. 지시사항을 따를 줄 알아야 한다(following direction). (자세한 것은 지난주의 기사를 참고 바람)
영진이의 경우 이 두 준비과정만 2개월이 걸렸다. 그 다음 단계로 SQRQCQ라는 수학 부 방법을 소개했다. 이 방법도 읽기 수준이 자기 학년에 와 있어야 가능하다.
수학은 주로 두 분야로 나누어져 있다. 개념과 방법이다. 수학의 개념은 ‘정연한 논리’로 서술되어 있다. 그러니 개념파악은 논리파악이다. 수학의 응용문제는 논리로 쓰여져 있고 특별한 분야이기 때문에 공부하는 방법도 특별하다. 이 공부 방법이 바로 SQRQCQ다. 이 방법은 수학의 계산 능력이 아니고 주로 응용문제 해결(논리 푸는 일)에 적용된다(Roy, 1998).
II. 수학 학습법-SQRQCQ(Survey, Question, Review, Question, Compute, Question)
문제개요 파악-첫 질문-다시 읽기-두 번째 질문-계산-최종 질문
A. 문제개요 파악(Survey)
응용문제의 감을 대강 잡기 위하여 빨리 한번 읽어본다. 그러나 아무렇게나 읽는 것이 아니고 무엇이 요구되며, 그 요구되는 사항이 몇이나 되는지 파악해야 한다.
B. 첫 질문(Question)
문제 자체를 이해했는지 자문하는 단계다. 이 자문에 충분히 대답을 못하면 문제를 정확히 파악했다고 볼 수 없다.
예: ‘42/84=1/2’를 계산하기는 쉬운데, 그 개념파악이 어렵다. 그 개념파악의 과정으로 벤 다이아그램(Venn diagram)을 쓴다. 이 개념을 자세히 거치면 답이 1/2가 된다. 이 마지막 벤 다이아그램에서 가운데 있는 숫자를 보고 그 관계와의 연결을 공부하게 한다. 여기서의 공통요소는 1, 2, 3, 6, 7, 14, 21, 42였다. 즉 최대공약수는 42이다. 우선 이 관계와 연결을 이해하면, 개념파악이 뚜렷하다.
C. 문제 다시 읽기(Review)
이것을 또 한번 읽을 때 학생이 필요로 하는 과정을 다시 정리하게 한다. 이때 가끔 그래픽 구성(graphic organizer)에서 순서적(sequence)으로 놓은 방법을 써서 여러 가지를 순서적으로 일일이 정리한다.
D. 두 번째 질문(Question)
두 번째 질문의 주목적은 어떤 방법으로 풀까?를 결정하게 된다. 즉, 어떤 수학 순서를 밟아야 할지, 적절한 풀이방법을 찾기 위한 순서이다. 이번은 고등학교 수준의 예이다. 100명의 학생이 캠핑을 갔다. 아침 식사 때 86명이 계란을 먹었고, 75명이 베이컨을 먹었다. 62명은 토스트를 먹었고, 82명이 우유를 마셨다. 그 중 몇 명이 계란, 베이컨, 토스트, 우유 네 가지를 다 아침 식사로 먹었나?(학생들이 모두 세 가지 이상은 먹었다.)
이 과정에서 위에서 말한 연결과 관계를 잘 아는 학생은 즉시 우선 계란, 베이컨, 토스트를 안 먹은 학생을 계산해 봐야겠다는 생각부터 든다. 이런 질문을 자기 자신에게 잘 하는 학생일수록 개념파악이 잘 되는 학생이다. 수학을 싫어하는 학생의 특징이 이 두 번째 하는 질문과정을 못한다. 필자가 독서 지도를 할 때, 이 두 번째 질문을 할 때가 되면, 으레 몇 명의 학생은 ‘그러면, 더하기인지, 곱하기인지만 가르쳐 주시면 나머지는 제가 알아서 할게요’라고 한다. 그런 학생을 다시 검토하여 보면, 첫 번째의 개념 파악하기가 미급하였고, 어느 정도 됐더라도 문자 그대로 ‘그냥 스쳐만’간 것으로, 첫 질문조차도 이해했는지 의문이다. 또 했더라도 질문을 한번 정도밖에는 하지 않았다. 그보다 더 큰 문제는 세 번째 읽는데 가장 중요한 문제가 있다. 다시 말하자면, 집을 지을 때, 기초나 기둥이 없이, 지붕을 올릴 수가 없다. 이때 겨우 임시변통으로 지붕이 올라갔더라도 튼튼한 집은 아니다. 그러니 다음 비슷한 수학 문제가 나오면, 그것을 해결하지 못 한다. 그렇게 때문에 준비가 안된 상태로 다음으로 넘어가지 말기를 바란다.
예로, 10-2=8의 개념이 없는 1학년 학생에게 이 것이 틀렸는지 맞았는지 알고 싶으면, ‘8+2를 해서 10이 되면 맞을 거야’라고 가르치면, 이 것은 개념파악으로 배운 것이 아니므로 암기만 한 것으로 왜 10-3=7인지 알 수 없다.
E. 계산(Compute)
기본이 굳고, 개념파악이 충분할 때 계산조율(calculating operation)을 한다. 즉, 계산은 개념파악이 아닌, 공식화되어 있는 방법(방정식 푸는 방법)이다.
F. 세 번째 질문(Question)
이 것은 문제의 답의 점검이다. 여기에는 두 가지 점검이 있다.
첫째 점검은 계산 조율의 정당성이고, 둘째는 다시 처음으로 돌아가서 문제가 요구하는 것이 무엇이냐를 다시 확인하고 그 답이 이 문제와 공통되었는지를 점검하여야 된다.
계산 조율의 정당성은 위의 예에서 ‘10-2=8이라면 (10-2)+2=(8)+2’가 ‘10=8+2’가 된다고 확증하면 계산 자체는 맞다고 볼 수 있다.
그러나 문제 개념파악으로 엉뚱한 대답이 나올 경우 이 수학 결론은 타당하다고 볼 수 없게 된다.
(추천독서 목록과 학습방법(Close reading도 포함 됨)이 자녀의 독서수준별로 된 것이 있습니다.)
문의 (909)861-7979
스마터리빙
more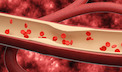 [ 건강]
[ 건강]이제 혈관 건강도 챙기자!
[현대해운]우리 눈에 보이지 않기 때문에 혈관 건강을 챙기는 것은 결코 쉽지 않은데요. 여러분은 혈관 건강을 유지하기 위해 어떤 노력을 하시나요?
 [ 건강]
[ 건강]내 몸이 건강해지는 과일궁합
 [ 라이프]
[ 라이프]벌레야 물럿거라! 천연 해충제 만들기
 [ 건강]
[ 건강]혈압 낮추는데 좋은 식품
[현대해운]혈관 건강은 주로 노화가 진행되면서 지켜야 할 문제라고 인식되어 왔습니다. 최근 생활 패턴과 식생활의 변화로 혈관의 노화 진행이 빨라지고
사람·사람들
more
인터뷰-한국어진흥재단… “한국어 확대 체계적으로”
차세대 한국어 및 한국문화 교육을 목표로 활동해 온 한국어진흥재단이 2026년 제16기 이사회에서 유니스 이 이사를 신임 이사장으로 선출하며 …

캘리포니아 태권도협회 이취임식
캘리포니아 태권도협회(CTU) 신년회 및 회장 이·취임식 행사가 지난 10일 오렌지카운티 한인회관에서 열렸다. 이날 행사에서는 용호재 관장이 …
1945년 해방둥이 모임 신년모임
올해로 창립 11주년을 맞은 1945년생 해방둥이 모임(회장 최용자)은 지난 10일 해피 노래교실에서 신년모임을 열고 회원 간 친목을 다졌다.…
전남대 남가주 동문회 신년회
전남대 남가주 총동문회(회장 차흥주)는 지난 10일 아리수 식당에서 동문과 가족들이 참석한 가운데 2026년 신년회를 개최했다. 이날 참석자들…
도산사업회 신년하례식 26일 아로마센터 5층
미주 도산안창호기념사업회(회장 데이빗 곽)는 오는 26일(월) 오후 5시30분 LA 한인타운 아로마센터 5층 더원 뱅큇홀에서 ‘2026 신년하…
많이 본 기사
- 차기 연준의장 인선 판도변화…해싯 지고 워시 부상
- 대법, 오는 20일 판결선고일로 예고…관세 결론 나올지 주목
- “모델 같은 얼굴, 재산 노렸나” 박나래 전 남친 사태..기안84 발언 ‘파묘’
- 트럼프 “그린란드 문제 협조 않는 나라에 관세 부과할 수도”
- 베네수 야권 지도자 “적절한 때 정부 인수…최대한 빨리”
- 운명의 한일전, 韓 4강 진출 시 확정... ‘어떻게 이런 행운이’ 日 준결승 선착, 승부차기 끝에 요르단 격파
- 대장암 위험 높이는 생활 속 잘못된 습관 5가지
- 징역 5년 선고에 굳은 얼굴, 입술 깨문 尹…법원 앞엔 지지자
- 트럼프 ‘차기 연준의장 유력’ 백악관 측근에 “현직에 두고싶어”
- 커쇼 은퇴 번복, WBC 전격 출전→류현진과 맞대결 가능성
- 식후 ‘블랙커피’ 한 잔, 당뇨약만큼 효과 있다
- 트럼프 “건강보험사 대신 개인에 보조… 1
- 국립공원 방문시 시민권·영주권 확인한다
- “방탄소년단 부산오는데 한 몫 잡자”..숙소비 10배→강제 취소까지 ‘논란’
- ‘결혼 17년 차’ 야노 시호, 정성껏 에르메스 골랐는데.. “필요 없다” 명품 거절한 추성훈에 충격
- 트럼프가 베네수 야권리더 만난날 CIA국장은 임시대통령 만나
- ‘트럼프 압박’에 손잡은 中·加…전기차·유채씨 관세 인하 합의
- 트럼프측근 연준의장후보 “파월수사, 단순 정보요청…별것없을것”
- 젤렌스키 “우크라 대표단, 안전보장 논의 위해 미국행”
- South Korea’s ‘Passport Power’ Remains in World’s Top Tier for 6th Straight Year
- 엘리베이터로 옮겼나, 사다리차로 옮겼나…김병기 금고 오리무중
- 가자지구 과도기 ‘행정국가위원회’ 카이로서 첫 회의
- 오픈AI, 미국서 챗GPT에 광고 도입…무료·저가요금제에 적용
- 美 “친미경제블록 구축…모든 양자관계에서 상업적 거래 추진”
- 치명적 독버섯 ‘데스캡’ 확산 비상
- 공립고교에 ‘풍물패 동아리’ 떴다
- 보모와 불륜 북VA 남성, 완전범죄 노리고…
- “박찬욱 ‘어쩔수가없다’, 미국서 韓영화 역대2위 흥행 예상”
- 자랑스러운 한인상에 아브라함 김 전 CKA 대표
- 종합특검법, 與주도로 국회 통과…지선까지 ‘특검수사’ 전망
- “대기자 명단 신청 접수하세요”
- 동포들 우롱하는 ‘글로벌 인재사업’
- ‘그린란드 담판’ 깨졌다… 덴마크·나… 2
- 자동차 재산세 폐지 법안 나올까
- 미, 그린란드 사려면 얼마 줘야하나?
- 하버 전 레이븐스 감독, 자이언츠 사령탑 부임 초읽기
- 신차 가격 고공행진… ‘100개월 할부’까지 등장
- 고가 주택 ‘찔끔’…저소득층은 ‘인상 폭탄’
- 자동차 재산세 폐지 법안 나올까 2
- 기대 수명 120세 시대… 알츠하이머는 최후의 불치병으로 남을까
- 미네소타서 또… 이민단속 저항 남성 … 1
- 결혼 앞둔 한국인 남성 태국 열차 사… 2
- 금리 하락에 전국 주택거래 회복세
- 타운 ‘팟홀’ 379개… “신고해야 … 2
- LA 올림픽 티켓 예약 열기 첫날부터 ‘후끈’
- [인터뷰] “당뇨, 몸이 보내는 신호 잘 살펴보고 대처”
- ‘별거 고백’ 슈, ♥임효성과 두 달 째 연락 두절.. “화해하고 파” 속내 고백
- 한국 ‘여권 파워’ 6년 연속 최상위권
- “맛있는 음식 저렴하게 즐겨볼까”…레스토랑 위크 시작
- “‘BTS 초청’ 선거 공약 현실이 됐어요”... ‘아미’ 멕시코 장관, 진과 만남 영상 공개
1/5지식톡

-
 한국 안경을 무료 배송으로 받아보실…
0
한국 안경을 무료 배송으로 받아보실…
0안녕하세요. 서울 안암동에 위치한 ‘보고싶다 안경원’입니다.저희는 다년간 한국 고객분들께 착용감 좋은 안경테와 한국안경브랜드,고압축 도수 렌즈를 합리적인 가격에 제공해온 안경 전문점입니다.이번에 해외 배송이 가능해…
-
 미 육군 사관학교 West Poin…
0
미 육군 사관학교 West Poin…
0https://youtu.be/SxD8cEhNV6Q연락처:wpkapca@gmail.comJohn Choi: 714-716-6414West Point 합격증을 받으셨나요?미 육군사관학교 West Point 학부모 모…
-
 ☝️해외에서도 가능한 한국어 선생님…
0
☝️해외에서도 가능한 한국어 선생님…
0이 영상 하나면 충분합니다!♥️상담신청문의♥️☝️ 문의 폭주로 '선착순 상담'만 진행합니다.☎️ : 02-6213-9094✨카카오톡ID : @GOODEDU77 (@골뱅이 꼭 붙여주셔야합니다…
-
 테슬라 자동차 시트커버 장착
0
테슬라 자동차 시트커버 장착
0테슬라 시트커버, 사놓고 아직 못 씌우셨죠?장착이 생각보다 쉽지 않습니다.20년 경력 전문가에게 맡기세요 — 깔끔하고 딱 맞게 장착해드립니다!장착비용:앞좌석: $40뒷좌석: $60앞·뒷좌석 …
-
 식당용 부탄가스
0
식당용 부탄가스
0식당용 부탄가스 홀세일 합니다 로스앤젤레스 다운타운 픽업 가능 안녕 하세요?강아지 & 고양이 모든 애완동물 / 반려동물 식품 & 모든 애완동물/반려동물 관련 제품들 전문적으로 홀세일/취급하는 회사 입니다 100% …
케이타운 1번가
오피니언

한인 2세들 ‘족쇄’ 국적법 신속 개정해야

노동법 준수로 공정의 새해 열자
 조지 F·윌 워싱턴포스트 칼럼니스트
조지 F·윌 워싱턴포스트 칼럼니스트 [조지 F. 윌 칼럼] 올 중간선거를 덜 불쾌하게 만드는 길
 최규성 삼성서울병원 이식외과 교수
최규성 삼성서울병원 이식외과 교수 [로터리] ‘토의 간’
 전병두 서북미수필가협회 회원
전병두 서북미수필가협회 회원 [금요단상] 꿀벌과의 인연
 심상용 / 서울대 미술관장
심상용 / 서울대 미술관장 [미술 다시보기] 모네와 연작의 경제학
 김정곤 / 서울경제 논설위원
김정곤 / 서울경제 논설위원 [만화경] 애플·구글 ‘적과의 동침’
 한 영 재미수필가협회 회장
한 영 재미수필가협회 회장 [한영의 독서칼럼] 햇살을 향해 헤엄치기
 이규민 한식진흥원 이사장
이규민 한식진흥원 이사장 [로터리] 시간을 담그는 문화, 한국의 장
1/3지사별 뉴스

뉴욕한인회‘제123주년 미주한인의 날’ 기념식 성황
뉴욕한인회(회장 이명석)가 13일 맨하탄 뉴욕한인회관에서 개최한‘제123주년 미주한인의 날’ 기념 행사가 각계에서 활동 중인 1.5세 및 2세…
국적이탈 수속에 2년이나 걸리다니⋯

연방의회서 “한인 위상·한미동맹 제고” 한목소리
한인 이민자들이 미국에 도착한 123주년을 기념하고 한인들의 미국 사회에의 기여를 알리는 ‘제 21회 미주 한인의 날’ 행사가 13일 연방의회…
보모와 불륜 북VA 남성, 완전범죄 노리고…

한미수교 100주년 기념 조형물 재설치 가능성 보인다
샌프란시스코 공원에 설치되어 있다 철거되어 창고에 보관중인 한미수교 100주년 기념 조형물이 다시 설치될 가능성이 열렸다.한국 국회 재정경제기…
재미한국학교협의회

오늘 하루 이 창 열지 않음 닫기 
















































.png)


댓글 안에 당신의 성숙함도 담아 주세요.
'오늘의 한마디'는 기사에 대하여 자신의 생각을 말하고 남의 생각을 들으며 서로 다양한 의견을 나누는 공간입니다. 그러나 간혹 불건전한 내용을 올리시는 분들이 계셔서 건전한 인터넷문화 정착을 위해 아래와 같은 운영원칙을 적용합니다.
자체 모니터링을 통해 아래에 해당하는 내용이 포함된 댓글이 발견되면 예고없이 삭제 조치를 하겠습니다.
불건전한 댓글을 올리거나, 이름에 비속어 및 상대방의 불쾌감을 주는 단어를 사용, 유명인 또는 특정 일반인을 사칭하는 경우 이용에 대한 차단 제재를 받을 수 있습니다. 차단될 경우, 일주일간 댓글을 달수 없게 됩니다.
명예훼손, 개인정보 유출, 욕설 등 법률에 위반되는 댓글은 관계 법령에 의거 민형사상 처벌을 받을 수 있으니 이용에 주의를 부탁드립니다.
Close
x