▶ 영재 교육-42, 수학 (I)
▶ 전정재 박사
그러나 학년이 올라 갈수록 수학에 영재라고 손꼽히던 진우의 수학 성적이 떨어지기 시작하더니 고학년이 되면서 수학에 별 취미가 없게 되었다. 과연 어찌된 일일까? 어려서 진우는 수학의 방법면(스킬, skills)을 너무 잘하는 학생이었다. 그러나 수학은 스킬만이 아이고 추상적인 개념(abstract thinking)을 파악하는 논리(logics)의 과목이다.
진우가 겪은 문제의 예를 들어보자. 82를 1/9로 나누면 그 답이 무엇이냐? 라는 문제가 있다. 아주 간단하다. 진우가 배울 때는 이런 문제가 있을 때 덮어놓고 ‘1/9이 9가 되려면 나누기 sign을 곱하기로 하면 된다’라는 방법을 단순히 기계적으로 배웠다. 그래서 진우는 누구보다도 빨리 82×9= 738이란 답을 할 수 있었다. 그러나 맞는 답일는지는 몰라도 ‘왜’ 그런 방정식이 쓰여졌는지 그 추상적인 개념 파악을 하지 못했다. 즉 82/(1/9)에서 문제는 (1/9)이다. 그러니 (1/9)를 중화(normalize)할 수 있는 방법은 9로 곱하면, 쉽게 다룰 수 있는 1로 변하고((1/9×9=1), 82×(9)/1이니 738/1로 변한다. 그러므로 정답은 738이다. 개념파악이란 것은 다루기 어려운 ‘1/9’를 어떻게 중화시키는가로 9를 곱하여 ‘1’로 만들었다. 그러나 ‘1’의 operational 정의(즉 ‘1’은 나누기나 곱하기에서 제자리이다)를 이해한 것이다.
필자가 처음 미국에 와서 대학 1학년 때 가장 잘했던 과목이 수학이었다. 숫자 개념에 워낙 어두웠는데도 대학 1학년, 처음 수학을 택하니 완전히 고등학교 때의 대수(algebra)나 미적분(calculus) 등 모두 복습하는 식이니 매우 쉬워 성적이 좋았다. 수학의 언어(숫자)를 미리 한국에서 배웠으니 영어를 몰라도 숨통이 터졌었다. 그러나 학기가 반도 못되어 A만 받던 필자는 헤매기 시작했다. 왜냐하면 처음 몇 주일은 한국식으로 외어서 하는 계산(rote calculation)이었으나 다음은 개념파악(conceptualization)으로 전개되는데 이것은 필자에게는 너무 생소했기 때문이다.
진우는 수학에서 필자 같이 개념을 알지 못한 채 스킬에만 능통하였다. 수학에서도 다른 언어 같이, 스킬의 기본방법(basic skills)을 배울 때와 스킬(skills)을 응용할 때로 나누어야 된다. 그러나 응용면으로 들어가기 전에 이 기본방법의 개념파악(conceptualization)을 하지 못하고는 응용면으로 들어가기가 매우 어렵다.
기본방법(basic skills)을 가르치는데는 다음 두 가지를 다루어야 한다.
1. 수학의 기본(basics) 자체를 가르쳐야 한다.
필자가 1학년 때 ‘더하기’ ‘빼기’ ‘곱하기’까지 외워 오라고 했던 기억이 난다. 구구단을 노래로 부르기까지 하던 기억이 난다. ‘9×9=81’이 노래의 가사가 아니라 ‘아홉(9)개’를 ‘아홉(9)번’ 되풀이하면 여든 하나(81)가 된다는 개념을 터득하였다. 집안 식구들에게 ‘9×9=81이 무엇’이라는 것(개념)을 한창 떠들고 났더니 옆에 있던 오빠가 ‘전씨 가문에 천재 났네’라고 놀리던 기억이 난다. 이런 기본(basics)을 우선 가르쳐야 수학의 오묘한 개념을 ‘이해’하게 된다. 개념을 모르고는 그 개념이 어떻게 쓰인다(응용)는 다음 단계로 들어갈 수가 없다. 어떤 방정식을 풀려고 할 때 이 방정식의 정체(statement)가 무엇이라는 것을 이해 못하고는 그 방정식을 어떤 operation을 이용해야 할지조차 알 수가 없다.
2. 이 기본개념을 이용하여 ‘생각’하는 방법을 가르친다.
종합능력(convergent reasoning), 판단력(evaluation), 창의력(divergent reasoning) 등을 배우는 것은 일반 언어(language)를 배우는 것과 동일하다. 즉 수학이란 다른 양상의 언어(logical language)이기 때문이다. 그렇다면 영재 교육의 경우 수학을 어떻게 이해하여야 되나?
■영재교육의 수학 커리큘럼
A. 수학방법(mathematical skills)은 어느 수준에서든지 가르친다. 저학년에만 속해 있는 것이 아니다.
B. 방법(skills)을 가르치는 데서만 끝나지 않고 개념파악, 연결성, 응용(개념파악의 시금석)에 중점을 둔다.
C. 저학년부터도 개념파악이 아무리 추상적이고 복잡하더라도 그 연결성, 응용을 잘만 가르치면 충분히 배울 수 있다.
D. 영재교육에서는 보통교육에서 받는 수학 시간의 스킬을 축소시켜 가르친다.
E. 어떤 고차원적인 추상적 수학 개념이라도 이를 이해할 수 있는 언어 능력이 있으면, 배울 수 있다. 응용문제를 못하는 것은 수학 실력이 없어서가 아니라 그 문제 자체를 이해할 수 있는 언어 실력이 부족하기 때문이다.
F. 영재수학 교육의 가장 중요한 목적은 스스로 생각하는 논리적인 능력을 발달시키는데 있다. 이는 방정식에 따라 수학을 풀어내는 것과는 정반대의 것이다.
G. 특히 영재교육에서 수학은 창의력을 기르는데 큰 역할을 한다. 좋은 예로, 영화 ‘Beautiful Mind’를 보면 내쉬(Nash) 박사가 사회적 문제(수학과는 전혀 다르게 보이는)를 수학으로 종합하고, 그 것을 수학 방법으로 해결책을 제시한 것이 결국 노벨상을 받는 창의력의 현상이 되었다. 이처럼 한 언어(사회적 문제)를 다른 언어(수학)로 전환시키는 것은 두 언어의 개념을 모르고서는 불가능한 일이다. 이것은 스킬이나 방정식에 따라 풀어놓은 수학과는 근본적으로 다른 양상이다.
H. 우리의 지성 발달은, 수학을 포함한 다음과 같은 단계를 거친다.
(i) 사물 판단의 단계(sensory motor stage)-이 시기의 특징은 a. 아직 말(수학)을 못하며, b. 사물(수학)을 판단할 때 그냥 보고, 그 차이점을 파악한다.
(ii) 배움의 준비시기(pre-operational stage)-이 시기의 특징은 a. 언어(수학)를 사용하기 시작하며, b. 언어(수학)를 사용해 사물을 배우기 시작하는데, c. 행동(수학 풀이)이 즉흥적이며, d. 자기 중심적이고, e. 한정되거나, 고정된 생각(수학)에 멈추어 있다.
(iii) 다각면의 생각 발달 시기(concrete operational stage)-시기의 특징은 a. 사물(수학)을 정리 정돈할 수 있고, b. 사물(수학)을 계산하고, 측정할 수 있으며, c. 사물의 다양한 면(수학의)을 알기 시작하고, d. 분석능력(수학)의 발달이 시작된다.
(iv) 창의력, 판단력 시기(formal operational stage)-이 시기의 특징은 a. 응용(수학)으로 새 것을 만들어낼 줄 알며, b. 상상력(수학)이 발휘하며, c. 가정(hypothesis, 수학적)할 줄 알고, d. 판단(수학적)을 한다.
I. 영재의 수학 스킬을 가르치는 주목적은 처음에는 주춧돌을 놓듯 기초(basics)를 가르치지만, 나중에는 이 모든 개념을 한데 묶는 개념을 알아야 한다. 방정식 같이 외워서 규격에 맞추는 과정이 아니고 이 과정에서 다른 영역을 새로 발견하는 일이다.
J. 다른 과목, 즉 과학(물리학, 화학, 생물학 등)의 논리계통(logical system)을 수학화 할 수 있으므로 이런 과학계통을 이해 내지 설명할 수 있다. 예로써 양자학(quantum mechanics)이다.
서론에서 소개한 진우는 능력이 탁월한 영재였음에도 불구하고 너무 일찍 수학을 외우는 것, 계산, 틀에 박힌 방정식 등으로 배우다가 고학년이 되면서부터 갑자기 추상적인 개념파악이니, 확률(probability), ‘짝 개념’(set theory) 등 ‘숫자로만’ 이해할 수 없는 세계를 접하자 완전히 당황할 수밖에 없었던 것이다. 필자 역시 대학 1학년 때 스킬(skills)에서 A+을 받았지만 개념 파악에 들어서 헤맸는데 그 원인은 단순히 영어를 잘 못해서가 아니라 사실은 생각하는 능력, 응용하는 능력 등이 부족했기 때문이었다. 다음 주는 이 개념파악(understanding of the number system) 발달에 대해 알아본다.
(추천독서 목록과 학습방법이 자녀의 독서 수준별로 된 것이 있습니다.)
문의 (909)861-7979
스마터리빙
more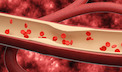 [ 건강]
[ 건강]이제 혈관 건강도 챙기자!
[현대해운]우리 눈에 보이지 않기 때문에 혈관 건강을 챙기는 것은 결코 쉽지 않은데요. 여러분은 혈관 건강을 유지하기 위해 어떤 노력을 하시나요?
 [ 건강]
[ 건강]내 몸이 건강해지는 과일궁합
 [ 라이프]
[ 라이프]벌레야 물럿거라! 천연 해충제 만들기
 [ 건강]
[ 건강]혈압 낮추는데 좋은 식품
[현대해운]혈관 건강은 주로 노화가 진행되면서 지켜야 할 문제라고 인식되어 왔습니다. 최근 생활 패턴과 식생활의 변화로 혈관의 노화 진행이 빨라지고
사람·사람들
more많이 본 기사
- 트럼프와 여성들 함께 찍힌 ‘엡스타인 사진’ 공개
- 비극 속 시민의 용기 총격범 맨손 제압
- 지구촌 또 ‘총기 난사’… 미·호주 잇단 참사
- ‘박성광♥’ 이솔이, 암 투병 중 안타까운 소식 “병원 몇 번 가는 건지..내 탓”
- 인니 수마트라섬 ‘대홍수’
- 시드니 유대인 총기참사 용의자는 50세 아버지·24세 아들
- 19개주, 전문직 비자 ‘10만불 수수료’ 소송
- 호주 총격범 제압 시민 영웅은 43세 과일가게 주인 아흐메드 씨
- 오늘 추첨 파워볼 잭팟 11억달러로 ‘껑충’
- 테슬라 11월 미국 판매… 4년만에 최저
- 워싱턴 한국학교협의회, 제37회 교사의 밤
- 안수화 회장 연임 확정
- 통계로 본 올해 대한항공… ‘캡틴 아메리카’ 가장 많이 보고, 최다 방문지 도쿄
- 항공기 승객정보 활용 추방 확대
- “성과는 있었지만 아직 끝 아냐”
- 버지니아, 도로 상태‘전국 2위’…MD 13위·1위 GA
- 팝핀현준, 수업 중 발언 논란에 교수직 사임… “진심으로 사과”
- 페어팩스 고교에 폭발물 소동…10월에 이어 두번째
- 새 회장에 유흥태·부회장 최인환 목사 선출
- 오늘의 베네수엘라가 내일의 동아시아국가…
- 총격 상처 피해 진학한 대학서 또 총기난사… “엄청난 타격”
- ‘아연’의 효과… 올바르게 복용하면 감기 기간 줄일 수도
- 뉴욕 백화점서 아기 기저귀 갈던 엄마, 정신질환자에 흉기피습
- [경제 트렌드] 외식비 줄이는 소비자… ‘팁 공포’ 한몫
- 박나래 ‘링거이모’, 진짜 ‘無면허’였다 “박나래 알지만 전혀 기억 안 나”
- 정우성 “현빈과 텐션 점점 무르익어”…사생활 변화엔 “말씀 못 드려”
- 중국 ‘여행자제령’ 직격탄 맞은 일본
- 워싱턴 지역 올 겨울 두 번째 눈
- “스마트폰 달고 사는 당신, 안구건조증 주의하세요!”
- “트럼프, 바이든 데자뷔인줄” 취임 1년새 고령 논란·지지율 뚝
- 투고(To Go) 해야 하나?
- 남가주한인부동산협회, 송년모임 개최
- 아이비리그 합격 가르는 것은 ‘스펙’ 아닌 ‘습관’
- MD 체육회장 입후보 등록 시작
- ‘계엄2수사단’ 노상원 1심서 징역 2년… “계엄 동력 엄중책임”
- 연방법원, 킬마르 석방 “적법한 추방 명령 없어”
- 뉴욕·뉴저지 등 19개 주정부 H-1B비자‘10만달러 수수료’소송
- 연말 DUI 집중 단속 무관용 강력 처벌
- 피로 얼룩진 주말…지구촌 곳곳 총격사건 잇달아
- 백악관 연회장 신축 저지 소송 국가역사보존단체, 연방지법에
- 퇴조의 핑크 타이드
- 관세가 끌어올린 물가… 가구당 1,200달러 추가 지출
- “걱정했잖아” 윤정수, 비 그친 발리서 ♥원진서와 신혼여행 만끽
- 중, 난징대학살 추도… ‘일본군 해골 베는 포스터’도
- [이민법 칼럼] 더 힘들어진 취업이민 1순위
- 모두가 원하는 물가 하락… 반드시 긍정적이지 않아
- 故 김지미에 금관문화훈장…마지막 말은 “보고싶다 사랑한다”
- 미, 베네수엘라 지상전 위협… 쿠바까지 흔들기
- 트럼프 관세 인하에도… 주요 식품 줄줄이 급등
- 제트블루 여객기, 카리브해 상공서 미군 급유기와 충돌 위기
1/5지식톡

-
 테슬라 자동차 시트커버 장착
0
테슬라 자동차 시트커버 장착
0테슬라 시트커버, 사놓고 아직 못 씌우셨죠?장착이 생각보다 쉽지 않습니다.20년 경력 전문가에게 맡기세요 — 깔끔하고 딱 맞게 장착해드립니다!장착비용:앞좌석: $40뒷좌석: $60앞·뒷좌석 …
-
 식당용 부탄가스
0
식당용 부탄가스
0식당용 부탄가스 홀세일 합니다 로스앤젤레스 다운타운 픽업 가능 안녕 하세요?강아지 & 고양이 모든 애완동물 / 반려동물 식품 & 모든 애완동물/반려동물 관련 제품들 전문적으로 홀세일/취급하는 회사 입니다 100% …
-
 ACSL 국제 컴퓨터 과학 대회, …
0
ACSL 국제 컴퓨터 과학 대회, …
0웹사이트 : www.eduspot.co.kr 카카오톡 상담하기 : https://pf.kakao.com/_BEQWxb블로그 : https://blog.naver.com/eduspotmain안녕하세요, 에듀스팟입니다…
-
 바디프렌드 안마의자 창고 리퍼브 세…
0
바디프렌드 안마의자 창고 리퍼브 세…
0거의 새제품급 리퍼브 안마의자 대방출 한다고 합니다!8월 23일(토)…24일(일) 단 이틀!특가 판매가Famille: $500 ~ $1,000Falcon: $1,500 ~ $2,500픽업 & 배송직접 픽업 가능LA…
-
 바디프렌드 안마의자 창고 리퍼브 세…
0
바디프렌드 안마의자 창고 리퍼브 세…
0거의 새제품급 리퍼브 안마의자 대방출 한다고 합니다!8월 23일(토)…24일(일) 단 이틀!특가 판매가Famille: $500 ~ $1,000Falcon: $1,500 ~ $2,500픽업 & 배송직접 픽업 가능LA…
케이타운 1번가
오피니언
 옥세철 논설위원
옥세철 논설위원오늘의 베네수엘라가 내일의 동아시아국가…

퇴조의 핑크 타이드
 조지 F·윌 워싱턴포스트 칼럼니스트
조지 F·윌 워싱턴포스트 칼럼니스트 [조지 F. 윌 칼럼] 대통령의 전쟁수행권
 조옥규 수필가
조옥규 수필가 투고(To Go) 해야 하나?
 신경립 / 서울경제
신경립 / 서울경제 [만화경] ‘뒷마당’ 찾겠다는 트럼프식 먼로주의

22기 LA평통 출범에 거는 기대

연말 시즌 사기·범죄 경계해야
 메건 매카들 워싱턴포스트 칼럼니스트
메건 매카들 워싱턴포스트 칼럼니스트 [메건 매카들 칼럼] 장편영화의 마지막 챕터인가
 김미선 서북미문인협회 회장시인
김미선 서북미문인협회 회장시인 [한국춘추] 하늘을 계산한 사람들, 칠정산
1/3지사별 뉴스

피로 얼룩진 주말…지구촌 곳곳 총격사건 잇달아
지난 주말 동안 미동부 아이비리그 브라운대학에서 총격 사건이 발생, 최소 2명이 사망하고 9명이 부상한데 이어 호주 시드니에서는 사망자 16…
뉴욕·뉴저지 등 19개 주정부 H-1B비자‘10만달러 수수료’소송

워싱턴 한국학교협의회, 제37회 교사의 밤
재미한국학교 워싱턴지역협의회(회장 정광미)가 13일 ‘제 37회 교사의 밤’을 개최, 한 해 동안 헌신한 교사들의 노고를 위로했다. 올해 최우…
안수화 회장 연임 확정

총격 상처 피해 진학한 대학서 또 총기난사… “엄청난 타격”
고교 총격 사건 생존자인 미아 트레타가 브라운대 총격 사건 이후 인터뷰하는 모습. [로이터]동부 브라운대에서 총격 사건으로 10여명의 사상자가…
내년 중간선거 낙관못하는 트럼프… “경제성과 전달에 시간 걸려”

오늘 하루 이 창 열지 않음 닫기 



















































.png)


댓글 안에 당신의 성숙함도 담아 주세요.
'오늘의 한마디'는 기사에 대하여 자신의 생각을 말하고 남의 생각을 들으며 서로 다양한 의견을 나누는 공간입니다. 그러나 간혹 불건전한 내용을 올리시는 분들이 계셔서 건전한 인터넷문화 정착을 위해 아래와 같은 운영원칙을 적용합니다.
자체 모니터링을 통해 아래에 해당하는 내용이 포함된 댓글이 발견되면 예고없이 삭제 조치를 하겠습니다.
불건전한 댓글을 올리거나, 이름에 비속어 및 상대방의 불쾌감을 주는 단어를 사용, 유명인 또는 특정 일반인을 사칭하는 경우 이용에 대한 차단 제재를 받을 수 있습니다. 차단될 경우, 일주일간 댓글을 달수 없게 됩니다.
명예훼손, 개인정보 유출, 욕설 등 법률에 위반되는 댓글은 관계 법령에 의거 민형사상 처벌을 받을 수 있으니 이용에 주의를 부탁드립니다.
Close
x